Daftar Isi ⇅
show
Himpunan
Himpunan adalah suatu susunan nilai yang beragam. Contoh mudahnya adalah buah-buahan yang dijual di toko buah dapat terdiri atas: mangga, sawo, jeruk, durian, dsb. Sementara itu di toko buah lain bisa jadi terdapat: manggis, pisang, semangka, mangga, dll. Dalam informatika, himpunan merupakan salah satu konsep penting karena kenyataannya, data yang harus diolah untuk menjadi informasi tidaklah bersifat tunggal.
Selalu terdapat irisan satu sama lain dan diperlukan pengolahan himpunan agar kita mampu menentukan suatu simpulan dan informasi lain sehingga data tersebut dapat memiliki nilai guna. Contohnya, ibu harus menentukan satu jenis buah yang harus dibeli agar dapat berhemat sehingga mendapatkan diskon pembelian dalam jumlah yang banyak. Kita dapat mengumpulkan data dari buah kesukaan semua anggota keluarga.
- Ayah menyukai = {pisang, rambutan, manggis, mangga}
- Adik menyukai = {mangga, durian, apel, nanas}
- Kakak menyukai = {melon, apel, mangga, sawo, semangka}
Dari beberapa himpunan di atas dapat kita ketahui bahwa terdapat irisan dari ketiga himpunan di atas, yakni buah mangga. Melalui informasi yang didapatkan dari pengolahan data berupa himpunan tersebut, Ibu dapat menentukan bahwa buah yang harus ia beli adalah buah mangga karena terdapat irisan jenis buah sama yang disukai oleh seluruh anggota keluarga.
Dalam praktiknya tentunya himpunan merupakan alat yang jauh lebih berguna dari sekedar membantu untuk membuat keputusan saja. Seluruh data yang kini diolah oleh berbagai aplikasi smartphone terbaru saja sejatinya berbasis himpunan dalam bentuk array dengan format JSON yang hilir-mudik antarserver dan perangkat lunak. Intinya, perangkat lunak terbaru kini memanfaatkan himpunan multidimensi yang bahkan dapat memiliki himpunan lain dalam setiap nilai himpunannya (multidimensional array).
Mengapa? Karena lagi-lagi, fakta objektif menunjukkan bahwa data yang diolah dalam sistem informasi dan komunikasi tidaklah bersifat tunggal dan pada kenyataannya terdiri atas banyak himpunan yang bisa jadi memiliki berbagai himpunan lain di setiap nilai himpunannya. Pengguna aplikasi memiliki parameter umur, jenis kelamin, teman, teman dari teman, kontak, kesukaan, keperluan rumah tangga, kotak pesan, dsb yang beragam namun tetap terkoneksi atau memiliki irisan terhadap nilai dan data lain di sekitarnya.
Sistem Bilangan
Dalam bidang komputer dan informatika, terdapat empat buah sistem bilangan yang umum digunakan, yaitu:
- sistem bilangan biner (bilangan berbasis 2),
- oktal (bilangan berbasis 8),
- desimal (bilangan berbasis 10), dan
- heksadesimal (bilangan berbasis 16).
Bilangan Desimal
Dalam kehidupan sehari-hari, bilangan yang pada umumnya digunakan adalah bilangan desimal seperti yang kita kenal selama ini. Ya, bilangan yang biasa kita gunakan terdiri atas angka satu hingga sepuluh yang terdiri atas angka: 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sisanya merupakan kombinasi dari kesepuluh nilai tersebut. Mudahnya, angka 12 adalah gabungan dari angka 1 dan 2, sementara itu 10 merupakan gabungan dari angka 1 dan 0.
Pada sistem bilangan desimal, digit yang pertama akan berubah ketika sebuah benda diletakkan di atasnya adalah digit yang berada pada posisi paling kanan. Digit tersebut akan berubah dari 0, 1, 2, 3, dan seterusnya hingga ada kemungkinan mencapai angka 9 (0009).
Jika ternyata bilangan 9 tersebut belum mencukupi, bilangan yang kedua dari kanan akan berubah dari 0 menjadi 1, sedangkan digit paling kanan kembali menjadi 0 (0010). Kemudian, digit paling kanan akan berganti lagi dalam rentang 0 sampai dengan 9.
Jika angka 19 ternyata belum mencukupi, digit kedua dari kanan akan berubah menjadi 2 dan digit paling kanan akan berganti menjadi 0 lagi (0020). Hal tersebut terus berlangsung hingga timbangan mencapai angka yang menunjukkan berat dari benda atau timbangan menunjukkan angka maksimalnya dengan 4 digit, yaitu 9999.
Bilangan Biner
Berbeda dengan sistem bilangan biner yang menggunakan 10 digit angka, bilangan biner yang digunakan pada sistem komputer hanya terdiri atas 2 digit, yakni 0 dan 1. Semua nilai yang dapat dihasilkan oleh bilangan desimal menggunakan 0 hingga 9 harus dapat diungkapkan melalui dua jenis angka saja. Bagaimana caranya? Berikut adalah beberapa contoh nilai angka desimal yang ditranslasikan ke bilangan biner, oktal, dan heksadesimal.
| Biner | Desimal | Oktal | Heksadesimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 8 | 10 | 8 |
| 1001 | 9 | 11 | 9 |
| 1010 | 10 | 12 | A |
| 1011 | 11 | 13 | B |
| 1100 | 12 | 14 | C |
| 1101 | 13 | 15 | D |
| 1110 | 14 | 16 | E |
| 1111 | 15 | 17 | F |
| dst | dst | dst | dst |
Menarik bukan? Ternyata selama ini sistem bilangan yang kita gunakan sehari-hari bukanlah satu-satunya sistem bilangan yang dapat digunakan. Terdapat banyak sistem bilangan lain bahkan sistem komputer kita hingga kini hanya dapat menggunakan sistem bilangan biner saja.
Lantas mengapa komputer menggunakan bilangan biner saja? Pertama, jawaban sederhananya dapat ditarik dari kembali bertanya kepada kita sebagai manusia yang hanya menggunakan sistem bilangan desimal dalam kehidupan sehari-hari.
Dapat kita bayangkan apabila kita menggunakan sistem bilangan biner pada mata uang yang kita gunakan bukan? Kita akan kesulitan untuk mengetahui dan menghitung nilai yang dibutuhkan untuk pembayaran apalagi memberikan kembalian. Begitu juga dengan sistem digital yang harus mampu serba berubah dan menyesuaikan data agar dapat diolah dan diaplikasikan pada beragam modul dan aplikasi yang beragam.
Sistem Bilangan Heksadesimal
Sistem bilangan heksadesimal menggunakan 16 macam simbol, yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C. D, E, dan F. Huruf-huruf A, B, C, D, E, F berturut-turut nilainya adalah 10, 11, 12, 13, 14, 15. Beberapa komputer menggunakan sistem, misalnya IBM System/360, Data General Nova, PDP — 1 1 DEC, Honeywell, serta beberapa komputer mini dan mikro.
Sistem heksadesimal mengorganisasikan memori utama ke dalam suatu byte yang terdiri atas 8 bit (binary digit). Setiap byte digunakan untuk menyimpan satu karakter alfanumerik yang dibagi dalam dua grup setiap bagian 4 bit. Jika satu byte dibentuk dari dua grup 4 bit, setiap bagian 4 bit disebut nibble. Empat bit pertama disebut high-ordernibble dan 4 bit kedua disebut low-order nibble (Natali, dkk, 2021, hlm. 84).
Konversi Bilangan Desimal menjadi Bilangan Biner dan Oktal
Meskipun kita menggunakan salah satu sistem bilangan, semua sistem bilangan sejatinya dapat diubah menjadi sistem bilangan lain atau biasa disebut sebagai konversi. Berikut merupakan langkah-langkah untuk mengonversi bilangan desimal (N10) menjadi basis atau sistem bilangan lain.
- Buatlah sebuah variabel untuk menampung bilangan hasilnya. Kita misalkan nama variabel tersebut adalah “hasil”.
- Bagi bilangan desimal (N10) menjadi basis atau sistem bilangan lain yang dituju.
- Catat sisa hasil bagi dari langkah 2 pada bagian terdepan (paling kiri) dari variabel “hasil”.
- Ganti bilangan desimal (N10) dengan hasil dari langkah 2.
- Ulangi langkah 2-4 sampai nilai N10 menjadi 0 (Natali, dkk, 2021, hlm. 40).
Agar lebih jelas, perhatikan gambar perumusan di bawah ini.

Berikut adalah pemaparan lebih lanjut dari masing-masing konversi bilangan desimal ke sistem bilangan lainnya.
Konversi Bilangan Desimal ke Bilangan Biner
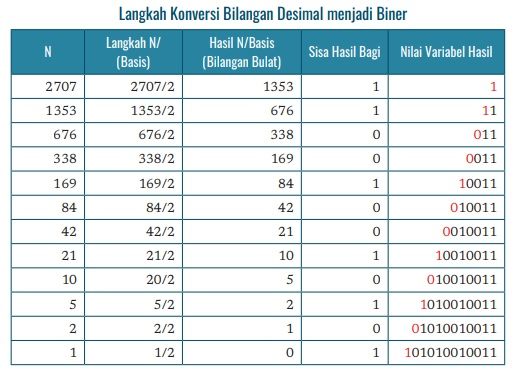
Pada tabel di atas, kolom “Nilai Variabel Hasil”, digit yang baru saja ditambahkan adalah digit yang diberi warna merah. Hasil akhir dari tabel tersebut adalah 101010010011. Untuk mempermudah penulisan dan proses baca, pada umumnya, digit-digit pada bilangan biner dituliskan per kelompok dimana setiap kelompok terdiri atas empat digit. Maka, 101010010011 dapat ditulis menjadi 1010 1001 0011.
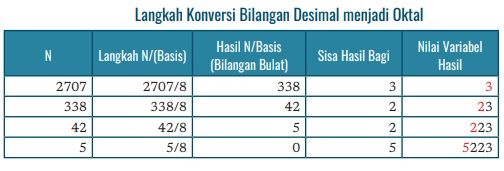
Konversi Bilangan Desimal ke Bilangan Oktal
Dengan langkah yang sama pada tabel sebelumnya, kita akan mengonversi bilangan desimal menjadi bilangan oktal.
Konversi Bilangan Biner dan Oktal menjadi Bilangan Desimal Setelah mengerti cara untuk mengonversi bilangan desimal menjadi bilangan biner dan oktal, tentunya, kita harus dapat melakukan konversi bilangan biner/oktal menjadi bilangan desimal. Agar lebih mudah untuk melihat hasil perhitungannya, kita akan mengonversi bilangan biner dan oktal yang sudah kita gunakan sebelumnya. Menurut Natali, dkk (2021, hlm. 42) caranya adalah sebagai berikut.
- melakukan perkalian terhadap setiap digit pembentuk sebuah bilangan dengan basis posisi. Posisi bilangan dihitung mulai dari digit paling kanan;
- menjumlahkan semua hasil perkalian tersebut.
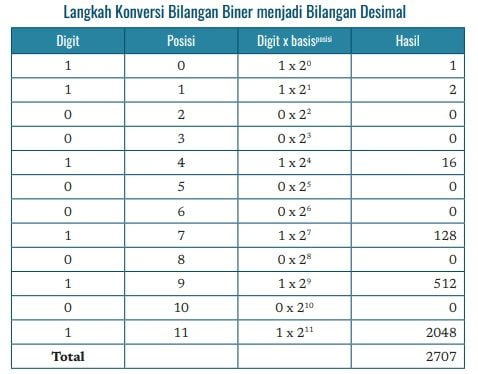
Konversi Bilangan Biner Menjadi Bilangan Desimal
Bilangan biner yang akan kita konversi menjadi bilangan desimal adalah 1010 1001 00112 . Kita akan menuliskan bilangan biner tersebut dalam sebuah tabel, dimulai dari digit paling kanan.
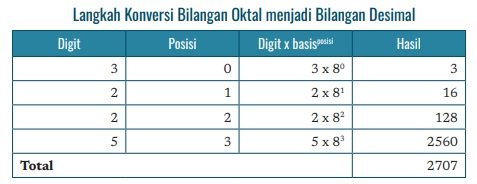
Konversi Bilangan Oktal Menjadi Bilangan Desimal
Saat ini, kita akan mencoba kembali melakukan konversi bilangan oktal menjadi bilangan desimal. Caranya sama dengan cara mengonversi bilangan biner menjadi bilangan desimal.
Bilangan oktal yang akan kita konversi ialah 52238 (ini adalah cara menuliskan bahwa 5223 adalah bilangan oktal atau basis 8).
Konversi Bilangan Heksadesimal ke Bilangan Lainnya
Seperti sistem atau basis bilangan lainnya, bilangan heksadesimal juga dapat dikonversikan ke sistem bilangan lainnya. Caranya sendiri di antaranya adalah sebagia berikut.
Konversi Bilangan Biner ke Heksadesimal
Ketika melakukan konversi bilangan biner ke heksadesimal (16 = 24 ), setiap 4 angka biner ekuivalen (setara) dengan satu angka heksadesimal. Contoh perhitungannya adalah sebagai berikut.

Konversi Bilangan Desimal ke Heksadesimal
Konversi bilangan desimal ke hexadesimal dapat dilakukan dengan membagi bilangan desimal dengan 16, hingga tidak bisa dibagi lagi. Contoh perhitungannya dapat dilihat pada table di bawah.

Konversi Bilangan Heksadesimal ke Desimal
Konversi bilangan heksadesimal ke desimal menggunakan perkalian setiap bilangan dengan basis yang dipangkatkan sesuai urutannya, kemudian hasilnya dijumlahkan. Contoh perhitungannya dapat dilihat pada table di bawah.

Konversi Bilangan Heksadesimal ke Biner
Untuk konversi bilangan heksadesimal ke biner, setiap 1 angka heksadesimal ekuivalen dengan 4 angka biner. Konversi setiap digit bilangan heksadesimal ke bilangan biner 4 digit, kemudian gabungkan. Jika terdapat digit 0 di depan hasil penggabungan bilangan biner, boleh dihilangkan. Contohnya adalah sebagai berikut.

Referensi
- Natali, dkk. (2021). Informatika smp Kelas VIII. Jakarta: Pusat Kurikulum dan Perbukuan Kemdikbudristek.
